NoSQL学习——文档数据库MongoDB(六)空间数据的读写与索引
# 空间数据模型
空间数据可用于表示很多物理模型,并可用于多种场景,例如与线下紧密结合的电商物流系统、包括地图在内的地理信息系统等。由于现实世界的空间模型具有一定的复杂性,且各层级的物体(例如省份边界线、城市道路等)数量庞大,空间信息的存储会相对复杂。
# 数据表示方法
空间数据一般用于描述点、二维形状、三维形状或更高维度的信息,因此,只通过一个基础类型的值进行描述是很难的,通过一个object进行描述更为自然,这就使得空间数据与MongoDB这类描述object的文档型数据库较为契合。
在描述空间数据时,需要首先建立坐标,常见的坐标系包括笛卡尔坐标系、极坐标系、球坐标系等,但无论在哪种数据库中,对于不同坐标系的支持都是存在的。在此基础上,点通常可以通过一组坐标值,即按一组坐标顺序排序的浮点数元组表示;一条线段可通过多个点的组合表示;在表示多边形时,则可以按照多个点连接后其线段一侧所围成的区域进行表示;进一步如果包含嵌套,则可以用多个多边形形成的区域进行布尔操作(通常可用与方法关联)得出。
这种描述在关系型数据库中需要转化为表格,通常需要一个独立的模块对数据进行抽象并建立相应的查询方法,例如将多边形的边与多边形的id关联、将点与边的关系分别存放在模块专用的表中,查找时通过联合查询返回多边形。
在MongoDB中,通常使用基于object的描述方法,特殊情况下也可以采用基于空间的方法,下面对其分别做简要介绍。基于空间的方法通常用于描述具有连续性质的地理性质,如温度、海拔、降水等,其方法是通过函数等计算将空间信息与位置进行关联。基于object的方法通常用于描述离散的实体,通过描述区域的边界表示该物体,例如地图上各省市的行政区划。
# 数据操作方法
空间数据的查询主要包含四类,集合操作、拓扑操作、方向查询和度量查询。集合操作即将空间物体视为集合,对其进行求交并补集等操作;拓扑操作是在此基础上,查询物体之间的重合、覆盖、连接等属性;方向和度量则分别用于查询物体之间的相对位置和距离。
空间数据是否相交等的计算可通过线性代数计算的结果得出;对于距离和方向,则可以通过坐标系的函数计算实现,在此先不做展开。下面只讨论拓扑关系如何实现计算。
在检查拓扑关系时,会采用一种九宫格式的矩阵进行检测,其方法是通过求不同部分的交集得出矩阵后根据矩阵的值进行判断。假设有一个如下所示的图,有一个物体A,其外部为,边界为,内部为。
__________
| _ U |
| |A| |
|__________|
判断A、B两物体是否相交使用的方法是用A的三个值分别对B的三个值进行与操作,如下公式所示,即计算A与B的内部、边界和外部是否分别重合。
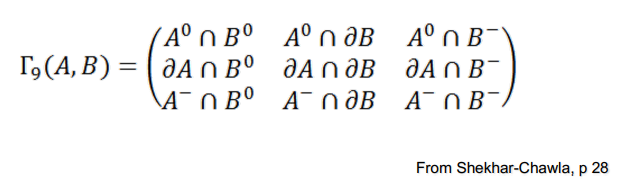
其结果的判断如下图所示为
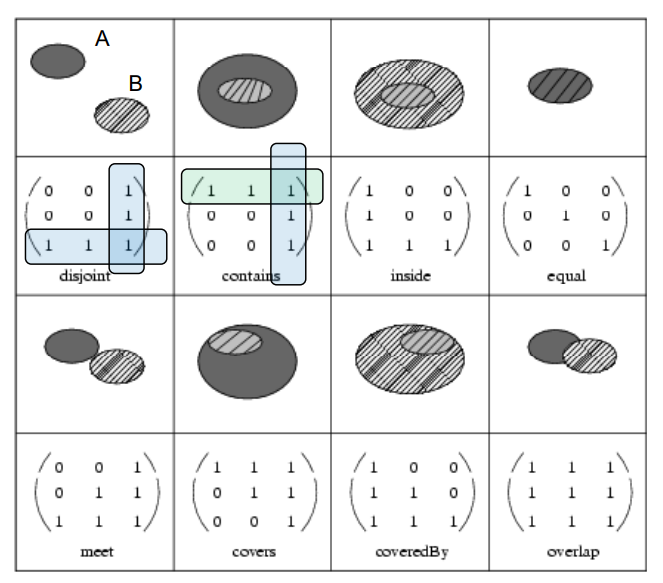
# 复合数据的查询
只针对空间数据本身的操作可能不具备足够的业务价值,因此,空间数据还需要结合其他非空间数据。在进行查询时,需要首先找到有关联的多个实体再计算相互之间的空间关系。空间数据的查询可包含选择性查询和范围查询,前者主要用于查找包含特定属性的物体之间的空间关系,后者则通常是查找某一范围内的物体。选择性查询时,通常通过扫描处理过的空间表实现;范围查找可以通过简单扫描实现,但并不高效,更好的方法是首先通过粗筛将完全不符合条件的物体筛除,再进行细致的查找,以此避免在全部数据上做耗时的判断。在多维的范围查询时,可通过多边形的最小边界与查询区域是否相交进行筛选,然后再通过其他算法计算实际的交集。另一种常见的查询是最近邻查找,可以通过全表扫描查询,但更好的方法是建立合适的索引然后查找。
# MongoDB空间数据查询
在MongoDB中,空间数据被存储在称为GeoJSON的结构中,或是坐标值元组中。前者使用的是类似地球的球面坐标,后者则表示平面中的数据。GeoJSON由OpenGIS定义,提供点、线条、多边形、点集、复合多边形等表示方法,通常格式为{type: "<GeoJSON type>", coordinates: <coordinates>},其中的坐标采用WGS1984标准,使用十进制的经纬度表示。
各类表示的数据结构如下:
- 点Point:
{type: "Point", coordinates: [x, y, ...]} - 线LineString:
{type: "LineString", coordinates: [[5, 5], [7, 5], ..., [5, 5]]},当最后一个坐标和第一个一致时,线条形成一个闭合路径。 - 多边形Polygon:
{type: "Polygon", coordinates: [[[5, 5], [7, 5], ..., [5, 5]], [[5, 6], [8, 5], ..., [4, 4]]]},与LineString的区别在于多边形可以通过多个多边形表示有空洞的形状。 - 点集MultiPoints:
{type: "MultiPoints", coordinates: [[5, 5], [7, 5], ..., [5, 5]]} - 复合多边形MultiPolygon:
{type: "MultiPolygon", coordinates: [[[[5, 5], [7, 5], ..., [5, 5]], [[5, 6], [8, 5], ..., [4, 4]]], [[[5, 5], [7, 5], ..., [5, 5]], [[5, 6], [8, 5], ..., [4, 4]]]]},即多个多边形,可以表示分散的多个多边形的组合。 - 几何数据集合GeometryCollection:
{type: "GeometryCollection", coordinates: [{type: "<GeoJSON type>", coordinates: <coordinates>}]},套娃其他几何数据,可用于在最外层表示。
在了解了数据定义后,我们终于可以开始了解实际的MongoDB空间数据查询。Mongo提供的空间数据查询包括:$geoNear和$geoNearSphere(查找一个点的最近邻),$geoWithin(查找指定形状内的所有几何体)和$geoIntersects(查找存在指定拓扑关系的几何体,如覆盖、相等、重合等关系)等。需要注意,空间查询同样分为查询和聚合。
$geoWithin,$geoIntersects:查询,通常格式是db.places.find({loc: {$geoIntersects: {$geometry: <GeoJSON>}}})。$geoNear:聚合,通常格式是:db.places.aggregate([ {$geoNear: {near: <Point>, distanceField: "dist.calculated", maxDistance: 2000, query: <criteria object>, includeLocs:"dist.location", spherical: <bool>}} ])
# 空间数据索引
由于空间数据的复杂性和大小都很高,索引在空间数据上甚至更为重要。空间索引的主要问题是如何组织几何体,由于这些几何体的空间大小相较于正常数据更大,实际存储的数据块能够容纳的几何体可能更少;另一方面,存储块可能需要存储相近的几何体。其中一种方法是基于块存储,将聚集在一起的几何体组织为一个块,然后对块建立索引。在这一过程中,分块的方法和索引的组织方式会分别影响IO速度和索引上的操作数量。
# 普遍的索引方式
# 1. 哈希索引
其中一种组织方式是哈希索引,通过哈希函数将块均匀地映射到存储块上。这种索引方式带来了常数级的查询时间,但只适用于单点查询。在MongoDB中,存储引擎提供了一种名为GridFile的类哈希索引方法,通过多个维度上的分隔,将空间数据按网格分块存储。这种网格不是均匀划分的,在每个维度上会根据不同区间内的几何体数量进行均分,即几何体越密集的地方,网格越密集。索引的结构表达为两个部分,一个表示块的多维数组和一组表示分界线的数组。例如,一个二维空间数据的索引结构表示如下:
| 0-12 | 12-20
14-20 | | B
4-14 | A | D
0-4 | C |
多维数组如下:
[
[,B],
[A,D],
[C,]
]
分界线数据:
{ X: [0, 12, 20], Y: [0, 4, 14, 20] }
这种索引用于点的单例查询时,只需要根据相关的性质(坐标、其他属性的索引)加载相应的数据块即可获得数据。在面对范围查找时,则需要加载所有与查询范围相交的块,然后再针对每个块内的数据查询相交点。在面对最近邻查找时,首先会加载查询点的数据块,然后查找块内数据,并查找相邻数据块,直到符合查找条件;或者不断扩大查找范围,加载更多数据块。
在插入过程中,哈希方法会查找所属的块进行插入。如果数据块的容量已满,则会创建新的数据块并导致索引重组。
# 2. 树索引
树索引主要通过树结构索引数据块,树的每个节点可以表示一个范围内的数值,其子节点则是对该空间划分后的子空间表示,常见的空间索引树有k维搜索树(kd-tree)、四叉树、R-树等。
K维搜索树
k维搜索树采用二叉树结构表示空间划分,例如对于一个二维空间,用根节点表示第一维的划分,用其子节点表示第二维的划分,在树的第三层又表示第一维,依此类推如下图所示,对于每个节点,其中都是用一个数值记录划分的边界值,可采用左闭右开的方式。这样做的好处是,通过新增叶子节点的数据块子节点并修改叶子节点的连接即可实现对数据块索引的重组,相较于哈希索引可能有更好的性能。level 1 x1(10) /(<) \(>=) level 2 y1(5) y2(6) / \ / \ level 3 x2(5) 数据块 x4(15) 数据块 ......- K维搜索树可以通过逐层判断实现单点查询,具体做法是使用每层对应的坐标查找下层节点的方向,直到找到叶子节点上对应的数据块,然后在其中查找需要的数据。
- 对于范围查询,索引树依然需要使用与哈希索引相似的手段进行查询,即查找到所有与查询范围重合的块,然后再在这些块中查找数据。
- 在最近邻查找中,首先需要在索引树上查找到查询点对应的数据块,然后寻找块当前最短距离,如果该距离与查询点形成的圆与其他块相交且数量不满足返回条件,则扩大查找范围。在经过几次重复后,达成数量或距离条件即可返回。
四叉树(Quad Tree)
四叉树的每个非叶子节点都记录了一个中心坐标,其四个子节点则可以分别表示东南、西南、东北、西北四个方向的划分,如果其子节点不再划分,则子节点就可以表示一个数据块,例如下图。level 1 n0(10, 10) /(SW) /(NW) \(SE) \(NE) level 2 n1(5, 5) 数据块 n3(15,5) 数据块 / / \ \ / / \ \ ......- 四叉树的查询仍然类似k维搜索树,因此不再赘述。
R-树(R-tree) R-树采用类似B+树的层级结构,但主要用于描述二维数据,其区别在于,R-树的键是最小边界矩形(Minimum Boundary Rectangle,MBR),即图形可以被该矩形覆盖而矩形面积最小,而B+树的索引键通常是一个数值。对于R-树,每个节点的子节点都是其可以覆盖的MBR(类似B+树中父母节点的范围覆盖子节点)。非叶子节点可以包含[n,m]个子节点,而叶子节点只对应一个图形及其MBR。由于多维空间的特性,一个小MBR的节点可以被多个大的节点包含,无论其层级。
由于具有与B+树相似的结构,R-树的操作与B+树相似:- 在查询点时,首先从根节点查询,依次查找子节点的MBR是否包含该点,如果包含,则进入该子节点,直到查询到叶子节点,否则可得出不存在的结果。
- 在进行范围查找时,则逐层比较MBR重合,从而找到MBR相交的叶子节点。
- 当一个节点的子节点数量由于添加新数据而超过子节点数量上限时,则对其进行拆分,拆分时要尽量减小新形成的MBR的面积,从而避免范围查询时搜索的子节点过多(叶子节点的MBR越大,上层的MBR越大,则与查询面积重叠越多)。
# 索引遍历的一种方法——空间填充曲线
空间填充曲线是一种将多维数据按某种特定顺序遍历,并形成一维索引的方法。遍历空间的曲线有很多,其中比较常见的有希尔伯特曲线和z型曲线。这些曲线会先将整个空间划分为多个可以通过平移重叠的子空间,例如对二维是4个空间。然后采用z型或u型曲线遍历,在此基础上,对子空间继续划分,对划分的空间采用相同的曲线遍历,直到不再能够进行划分,将子空间逐级首尾相连,就能够形成一条填充曲线。在进行编码时,会根据各个维度的数字坐标转化为二进制,然后依次连接起来再转化为10进制数,即为对应的一维坐标。通过这种索引方法,可以实现在一维空间中保留节点一定局部性的效果,但也会使得部分相邻节点在一维索引上相隔较远。
# MongoDB的方法
MongoDB使用名为2dsphere的索引,用于支持所有空间查询。创建的方法是在类型为GeoJSON的域上指定索引名为2dsphere:db.places.createIndex( {<indexField>: "2dsphere"} )。2dsphere索引采用了离散全局网络和B+树结合的方法,首先将几何区域划分为多个粒度的网格,然后使用B+树对每层网格进行索引。这种方式能够结合两种索引的一部分优点,但有存储上的损失。
# 总结
本章我们简单探索了MongoDB的空间数据表示方法和查询方法,并对空间数据建模和索引方法进行了一些探索。至此,我们就完成了对MongoDB大部分使用场景、使用方法及技术原理的大致了解。